Cách Lập Bảng Xét Dấu Giá Trị Tuyệt Đối

Kiến thức Lý thuyết với bài tập dấu nhị thức bậc nhất

Lý thuyết cùng bài tập vết nhị thức hàng đầu

1. Định lí về vết nhị thức bậc nhất1.1. Nhị thức số 1 là gì?

Nhị thức hàng đầu là những biểu thức tất cả dạng $ ax+b $, trong những số ấy $ a ≠ 0 $. Cho một nhị thức bậc nhất $ f(x)=ax+b $ thì số $ x₀ = -b/a $ làm cho $ f(x)=0 $ được call là nghiệm của nhị thức hàng đầu.

Bạn đang xem: Cách lập bảng xét dấu giá trị tuyệt đối

1.2. Định lí về dấu nhị thức bậc nhất

Bây tiếng, chúng ta viết lại nhị thức $ f(x) $ thành < f(x)=aleft(x-x_0right) > Dễ thấy, Khi $ x>x_0 Leftrightarrow x-x_0>0$ thì $ f(x) $ cùng thông số $ a $ cùng dấu với nhau, trở lại, khi $ xnhị thức bậc nhất

Cho nhị thức $ f(x)=ax+b $ với $ ane 0 $ thì

$ f(x) $ cùng vệt cùng với thông số $ a $ với đa số $ x >-b/a, $$ f(x) $ trái vệt với hệ số $ a $ với mọi $ x

Để dễ dàng lưu giữ, ta lập bảng sau và sử dụng luật lệ lớn thuộc – bé nhỏ khác, tức là ứng cùng với các giá trị của $ x $ ở bên bắt buộc nghiệm $ x_0 $ thì $ f(x) $ và hệ số $ a $ tất cả cùng vệt, còn ở phía bên trái thì ngược lốt với thông số $ a $.

Bảng xét vết của nhị thức bậc nhất

Cụ thể, cùng với ngôi trường đúng theo $a>0$ bọn họ gồm bảng xét lốt của $f(x)$ như sau:

còn Khi $a2. lấy một ví dụ vệt của nhị thức bậc nhất

ví dụ như 1. Xét vết biểu thức $ f(x)=3x+6 $.

Hướng dẫn. Ta tất cả $ 3x+6=0 Leftrightarrow x=-2. $ Hệ số $a=3$ là số dương, phải ta có bảng xét vệt sau đây:

Như vậy, $ f(x)>0 Leftrightarrow xin (-2,+infty) $, $ f(x)0 Leftrightarrow xin (-infty;frac13) $, $ f(x)3. Ứng dụng định lý vết của nhị thức bậc nhấtXét vệt các biểu thức bao gồm dạng tích — thương những nhị thức số 1, từ bỏ đó sử dụng nhằm giải bất phương trình hoặc điều tra hàm số.Lập bảng phá dấu giá trị hoàn hảo nhất.3.1. Cách lập bảng xét vết của tích, thương những nhị thức bậc nhất

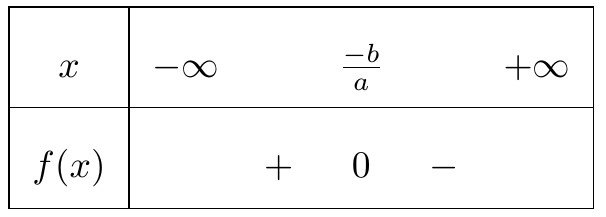
Để xét dấu của biểu thức $ P(x) $ gồm tích hoặc tmùi hương các nhị thức hàng đầu, ta thực hiện nhỏng sau:

Tìm những nghiệm của từng nhị thức số 1 tạo cho $ P(x) $, Tức là tìm nghiệm hoặc phần đa điểm tạo cho $ P(x) $ không xác minh (tức nghiệm của chủng loại thức, ví như có): $ x_1,x_2,dots,x_n $.Lập bảng xét vết của $ P(x) $ bao gồm có:Dòng đầu tiên tất cả những quý giá $ x_1,x_2,dots,x_n $ được bố trí theo thiết bị từ bỏ từ bỏ bé xíu mang đến lớn.Các dòng tiếp sau thứu tự là những nhị thức với lốt của chúng.Dòng sau cùng là lốt của $ P(x) $, thực hiện luật lệ nhân dấu đang học làm việc cấp cho II (Tức là số dương nhân số dương ngay số dương, số âm nhân số âm ngay số dương,…)

Ví dụ 3. Lập bảng xét vệt biểu thức < P(x)=(x-1)(x+2) >

Hướng dẫn. Trước tiên, bọn họ tìm kiếm nghiệm của từng nhị thức, có:

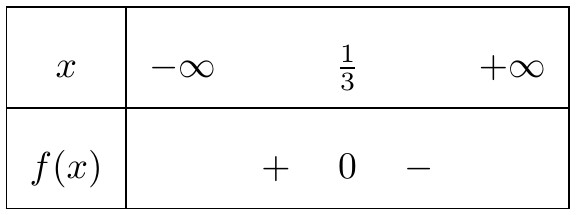
$ x-1=0 Leftrightarrow x=1, $$ x+2=0 Leftrightarrow x=-2. $

Sau kia, ta lập bảng xét dấu của $ P(x) $ nhỏng sau:

Chụ ý.

Xem thêm: Cách Làm Quần Cho Búp Bê Đơn Giản Nhất Không Cần May, Cách Làm Quần Áo Búp Bê

Để soát sổ vệt của một khoảng chừng làm sao $(a;b)$ kia đúng họ chỉ cần lựa chọn một giá trị $ x_0 $ bất kể trực thuộc khoảng $ (a,b) $ với tính giá trị của $f(x_0)$ đó.

lấy ví dụ 4. Lập bảng xét vết của biểu thức $$f(x)=(x+2)(x^2+5x-6).$$

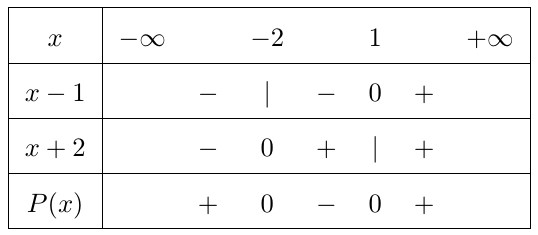
Hướng dẫn. Chúng ta chuyển biểu thức $f(x)$ về tích những nhị thức số 1 bằng phương pháp so với $x^2+5x-6=(x-1)(x+6)$. Do đó, biểu thức $f(x)$ trnghỉ ngơi thành$$f(x)=(x+2)(x-1)(x+6)$$ Bảng xét vệt như sau:

Ví dụ 5. Lập bảng xét lốt của biểu thức $$g(x)=fracx+1x-7.$$

Hướng dẫn. Chúng ta có

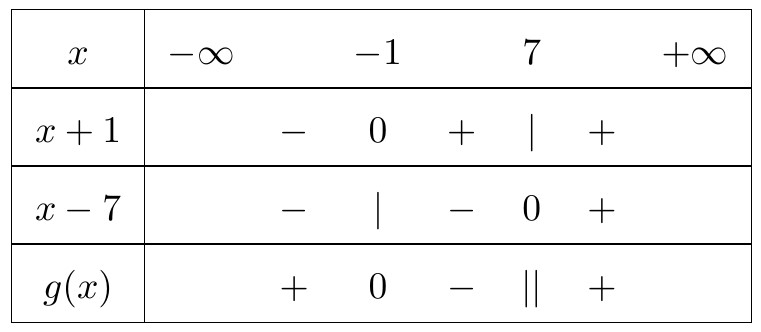
$ g(x) $ không xác minh khi $ x=7;$$ g(x)=0 Leftrightarrow x=-1$

Từ kia có bảng xét vết nlỗi sau:

ví dụ như 6. Lập bảng xét vệt của biểu thức < h(x)=frac1x+2-frac3x+4 >

Hướng dẫn. Rõ ràng biểu thức $ h(x)$ chưa có dạng tích/thương thơm những nhị thức số 1, buộc phải chúng ta cần quy đồng giữ giàng mẫu mã của biểu thức đó. Cụ thể nhỏng sau $$h(x)=frac-2(x+1)left( x+4right) left( x+2right) $$

Từ đó lập được bảng xét dấu như hình vẽ tiếp sau đây (có thể ghnghiền mẫu $-2$ vào với $x+1$ thành $-2x-2$):

Một số chú ý Lúc lập bảng xét vết một biểu thức:Dấu của những biểu thức $ (ax+b)^2n $ luôn luôn là vết dương hoặc bởi ko, chỉ bằng ko tại từng $ x=-b/a. $Dấu của những biểu thức $ (ax+b)^2n+1 $ luôn cùng vệt cùng với nhị thức $ ax+b. $Nếu biểu thức $ f(x) $ chỉ tất cả tích hoặc thương những nhân tử tất cả dạng $ (ax+b)^n $ cùng với số nón lẻ (tức $f(x)$ chỉ có nghiệm đối chọi hoặc nghiệm bội lẻ) thì vết của $ f(x) $ đang tuân thủ theo đúng quy phương pháp đan lốt. Do kia, vào thực hành ta chỉ cần lập bảng xét vệt bao gồm hai loại, hoặc vẽ trục xét vệt, chẳng hạn biểu thức $h(x)$ ngơi nghỉ trên rất có thể lập bảng xét dấu ngắn gọn gàng nlỗi sau:

3.2. Sử dụng vệt nhị thức số 1 giải bất pmùi hương trình tích, bất pmùi hương trình thương

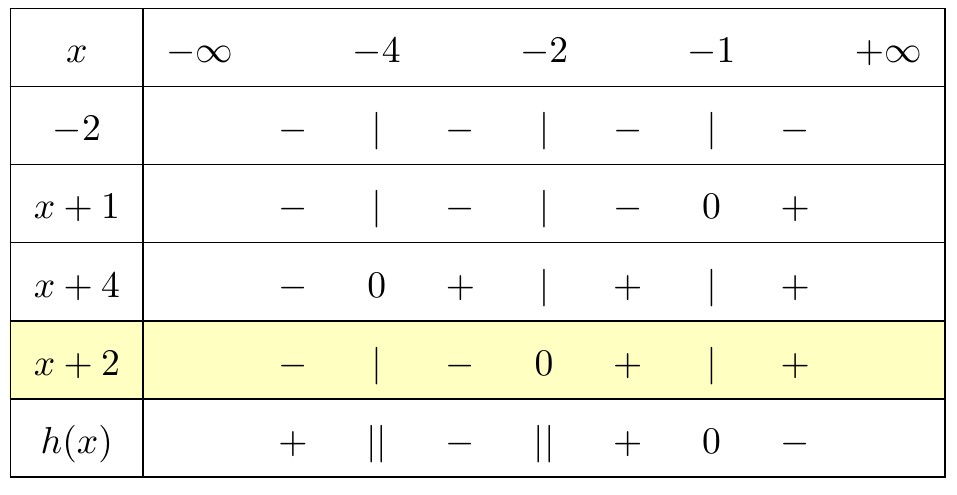
Phương thơm pháp chung nhằm giải các bất phương thơm trình tích, thương là:

Tìm ĐK xác định và quy đồng ko quăng quật mẫu mã những phân phức.Phân tích bất phương thơm trình các thành tích, thương thơm các nhị thức bậc nhất.Lập bảng xét vệt mang đến bất phương thơm trình cùng Tóm lại nghiệm.

Xem thêm: Cách Làm Muối Xí Muội Đà Lạt, Cách Làm Món Muối Ớt Xí Muội Của Bòn Bon

Ví dụ 7. Giải bất phương thơm trình sau: $$ (2x-3)(4-5x)+(2x-3)>0 $$ Hướng dẫn. Biến đổi bất pmùi hương trình thành beginalign &-5left( x-1right) left( 2x-3right) >0 Leftrightarrow &left( x-1right) left( 2x-3right)$ (2x+3)^2-(x-2)^2 geqslant 0 $$ (x-3)^4-1 leqslant 0 $$ frac1x >1 $$ fracx+23x-1 geqslant -2 $$ frac30x+1-frac24x+2+frac3x+3+1 >0 $

Sau Lúc đang học tập cả lốt tam thức bậc hai, những em hoàn toàn có thể tìm hiểu thêm đoạn Clip sau:

3.3. Sử dụng dấu nhị thức hàng đầu giải bất pmùi hương trình cất vệt quý hiếm giỏi đối

Về phương thơm trình đựng vết quý giá tuyệt vời nhất xin mời các bạn xem tại trên đây Pmùi hương trình đựng trị hay đối

Bất pmùi hương trình cất ẩn trong dấu quý hiếm tuyệt vời nhất cơ bản

Bằng phương pháp áp dụng đặc thù của cực hiếm hoàn hảo ta hoàn toàn có thể dễ dàng giải những bất phương trình dạng $|f(x)| a$ cùng với $a>0$ mang lại trước.

$ |f(x)| $ f(x)>a Leftrightarrow left< beginarrayl f(x)a endarrayright.$Bất phương trình những vết cực hiếm hoàn hảo và tuyệt vời nhất cơ bản

Chúng ta lập bảng khử lốt cực hiếm tuyệt vời, cụ thể về phương thức này xin mời các bạn coi một ví dụ sau: