CÁCH TÍNH TÍCH PHÂN TỪNG PHẦN
Ngulặng hàm tích phân là 1 trong những trong số những văn bản quan trọng thường xuyên lộ diện trong đề thi xuất sắc nghiệp trung học phổ thông đất nước để xét vào đại học. Nếu đã nắm vững phần nguyên hàm thì Việc tính tích phân xác định với cách thức tích phân từng phần sẽ khá dễ ợt cùng với các em.
Bạn đang xem: Cách tính tích phân từng phần
Vậy cách làm cách tính Tích phân từng phần như thế nào? Bài viết dưới đây, bọn họ đã cùng mày mò các dạng bài thói quen tích phân xác định mà lại ta đề xuất vận dụng phương pháp tích phân từng phần để giải, qua đó, giải những bài xích tập minch họa nhằm các em hiểu rõ hơn.
I. Tích phân từng phần, công thức, bí quyết tính
• Nếu u(x) cùng v(x) là những hàm số tất cả đạo hàm cùng tiếp tục trên
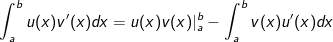
hay
• Áp dụng phương pháp trên ta có phương pháp tính tích phân từng phần nlỗi sau:
- Cách 1: Viết f(x)dx dưới dạng udv = uv"dx bằng phương pháp lựa chọn 1 phần phù hợp của f(x) làm cho u(x) và phần sót lại dv = v"(x)dx.
- Bước 2: Tính du = u"dx và v = ∫dv = ∫v"(x)dx
- Bước 3: Tính
> Lưu ý: Phương pháp tích phân từng phần hay được áp dụng lúc hàm dưới dấu tích phân là tích của nhị một số loại hàm số không giống nhau (nhiều thức - logarit, nhiều thức - lượng giác, lượng giác - hàm mũ,...).
Xem thêm: Cách Di Chuyển Layer Trong Photoshop, Các Cách Di Chuyển Trong Ps
II. Một số dạng bài xích tập vận dụng tích phân từng phần thường xuyên gặp
• Tính tích phân hàm nhiều thức P(x) và hàm logarit nepe (lnx):
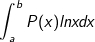
- Ta đặt u = lnx, dv = P(x)dx
• Tính tích phân hàm nhiều thức P(x) và hàm lượng giác (sinx; cosx):
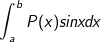
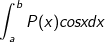
- Ta đặt u = P(x), dv = sinxdx (hoặc dv = cosxdx)
• Tính tích phân hàm nón (ex) và hàm lượng giác (sinx; cosx):
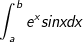
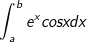
- Ta đặt u = ex , dv = sinxdx (hoặc dv = cosxdx). Tính nhì lần
• Tính tích phân hàm mũ (ex) với hàm đa thức P(x):
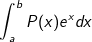
- Ta đặt u = P(x) , dv = exdx
III. Bài tập tích phân từng phần có lời giải
* Những bài tập 1: Tính các tích phân sau bằng phương thức tích phân từng phần
* Lời giải:
Đặt
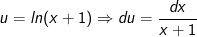
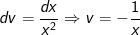
- Áp dụng công thức tích phân từng phần, ta có:
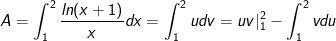
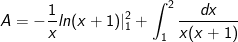
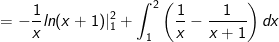
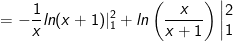
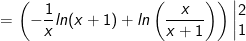
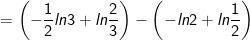
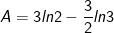
- Đặt
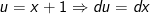
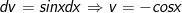
- Áp dụng phương pháp tích phân từng phần ta được:
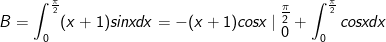
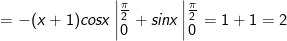
Vậy B = 2.
- Đặt
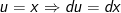
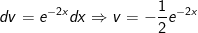
- Áp dụng cách làm tính tích phân từng phần ta được
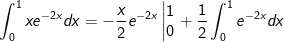
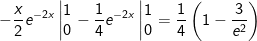
Vậy
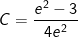
- Đặt
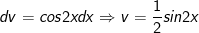
- Áp dụng cách làm tích phân từng phần ta được:
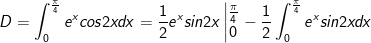
- Xét:
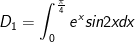
- Đặt
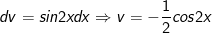
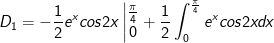
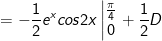
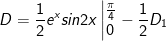
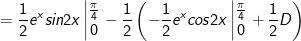
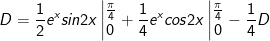
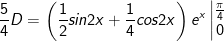
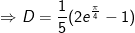
* bài tập 2: Tính tích phân sau:
* Lời giải:
- Ta đặt:
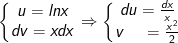
- lúc kia, ta có:
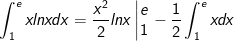
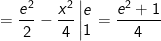
- Ta có:
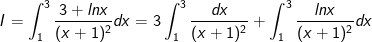
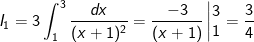
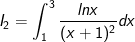
- Ta đặt:
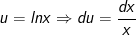
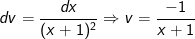
- Áp dụng phương pháp tích phân từng phần, ta được:
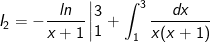
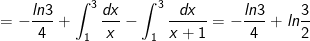
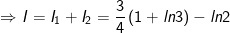
* Những bài tập 3: Tích các tích phân
* Lời giải:
- Đặt
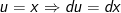
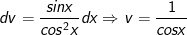
- Áp dụng bí quyết tích phân từng phần:
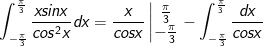
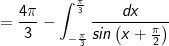
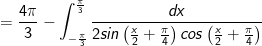
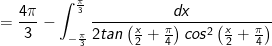
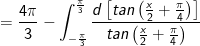
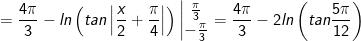
- Đặt
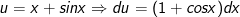
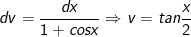
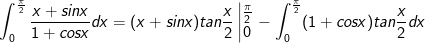
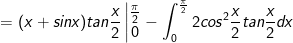
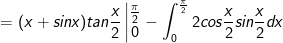
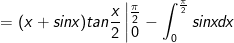
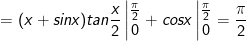
IV. bài tập tích phân từng phần từ giải
* các bài tập luyện 1: Tính các tích phân sau:
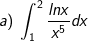
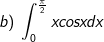
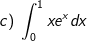
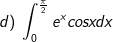
* những bài tập 2: Tính những tích phân sau:
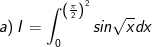
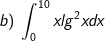
* Hướng dẫn:
a) Đặt
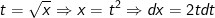
b) Ta có:
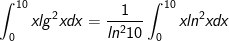
Xem thêm: Cách Viết Tài Liệu Hướng Dẫn Sử Dụng Phần Mềm Quản Lý Văn Bản
* bài tập 3: Tính các tính phân sau:
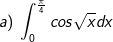
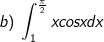
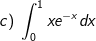
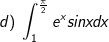
* Bài tập 4: Tính những tính phân sau:
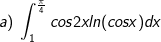
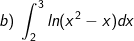
* Hướng dẫn:
a) Đặt u = ln(cosx)dx → du = (-sinx/cosx)dx,
dv = cos2xdx → v = sin2x/2
b) Đặt u = ln(x2 - x) → du =?; dv = dx → v = ?
vì thế, cùng với nội dung nội dung bài viết về tích phân từng phần cùng bài xích tập có giải thuật nghỉ ngơi trên, bài toán quan trọng đặc biệt duy nhất là các em buộc phải nhớ đặt u là gì cùng dv là gì để dễ dãi câu hỏi tính được du cùng lựa chọn nguyên ổn hàm v. Thông thường nếu đặt đúng u cùng dv thì ta đang thấy tích phân chiếm được đã dễ dàng tính rộng, nếu để không nên thì tích phân chiếm được đang khó khăn hơn tích phân ban sơ.