Khoảng cách giữa điểm và đường thẳng
Công thức tính khoảng cách thân 2 điểm, tốt phương pháp tính khoảng cách tự điểm tới con đường trực tiếp được thực hiện phổ cập trong hình học.
Bạn đang xem: Khoảng cách giữa điểm và đường thẳng
Không những thế, phương pháp tính khoảng cách giữa 2 điểm, tính khoảng cách tử điểm tới mặt đường thẳng còn là đại lý để các em tính được khoảng cách giữa 2 mặt đường thẳng, giữa 2 khía cạnh phẳng với khoảng cách từ điểm tới mặt phẳng.
Bài viết này họ thuộc ôn lại công thức tính khoảng cách thân 2 điểm, trường đoản cú điểm tới đường trực tiếp, thông qua đó áp dụng giải một số trong những bài tập minh họa nhằm những em nắm rõ giải pháp vận dụng bí quyết tính này.
I. Công thức tính khoảng cách thân 2 điểm
- Cho điểm A(xA; yA) với điểm B(xB; yB), khoảng cách thân hai đặc điểm này là:
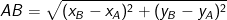
II. Công thức tính khoảng cách trường đoản cú điểm cho tới mặt đường thẳng
- Cho mặt đường thẳng Δ: Ax + By + C = 0 và điểm M0(x0; y0). khi đó khoảng cách trường đoản cú điểm M0 cho con đường trực tiếp Δ là:
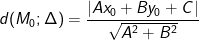
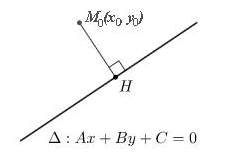
> Lưu ý: Trong ngôi trường hợp đường thẳng Δ chưa viết dưới dạng tổng quát thì thứ nhất ta bắt buộc gửi mặt đường trực tiếp Δ về dạng bao quát.
III. Tính khoảng cách thân 2 điểm, từ bỏ điểm cho tới mặt đường trực tiếp qua bài bác tập minh họa
* lấy ví dụ như 1: Trong phương diện phẳng Oxy mang lại điểm A(1;2) với điểm B(-3;4). Tính độ lâu năm đoạn trực tiếp AB.
* Lời giải:
- Độ dài đoạn thẳng AB là khoảng cách thân 2 điểm A,B ta có:
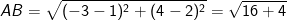
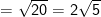
* lấy một ví dụ 2: Tính khoảng cách từ bỏ điểm M(2;-1) cho đường thẳng (Δ): 3x + 4y + 7 = 0.
* Lời giải:
- Khoảng phương pháp tự điểm M mang lại con đường thẳng (Δ) là:
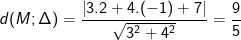
* ví dụ như 3: Tính khoảng cách trường đoản cú điểm A(0;1) đến con đường trực tiếp (Δ): 4x + 3y = 6
* Lời giải:
- Đường trực tiếp (Δ): 4x + 3y = 6 ⇔ 4x + 3y - 6 = 0
- Khoảng cách tự điểm A mang đến (Δ) là:
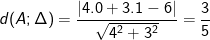
* lấy ví dụ như 4: Tính khoảng cách trường đoản cú điểm M(1;1) mang đến con đường thẳng (Δ) bao gồm phương trình ttê mê số: x = 3 + 3t với y = 2 + t.
* Lời giải:
- Ta yêu cầu đưa phương thơm trình đường trực tiếp (Δ) về dạng tổng quát.
Xem thêm: Game Đánh Bài Xập Xám Đơn Giản Dễ Hiểu, Mậu Binh Trên App Store
- Ta có: (Δ) trải qua điểm A(3;2) cùng có VTCP..
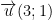
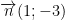
⇒ Pmùi hương trình (Δ): 1.(x - 3) - 3(y - 2) = 0 ⇔ x - 3y + 3 = 0
⇒ Khoảng biện pháp trường đoản cú điểm M(1;1) đến (Δ) là:
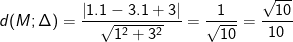
* lấy ví dụ 5: Đường tròn (C) có tâm là cội tọa độ O(0; 0) và xúc tiếp với mặt đường thẳng (Δ): 4x - 3y + 25 = 0. Bán kính R của mặt đường tròn (C) bằng:
* Lời giải:
- Do đường thẳng (Δ) tiếp xúc cùng với mặt đường tròn (C) yêu cầu khoảng cách tự chổ chính giữa đường tròn mang lại mặt đường thẳng (Δ) đó là bán kính R của con đường tròn.
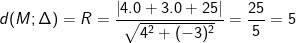
* ví dụ như 6: Khoảng bí quyết từ giao điểm của hai tuyến đường thẳng (d1): x - 3y + 4 = 0 và(d2): 2x + 3y - 1 = 0 cho đường trực tiếp ∆: 3x + y + 16 = 0 bằng:
* Lời giải:
- Trước hết ta buộc phải tra cứu giao điểm của (d1) với (d2); tự kia tính khoảng cách từ giao điểm này cho tới (∆).
- Giả sử giao điểm của (d1) với (d2) là A thì tọa độ của A là nghiệm của hệ phương thơm trình:
x - 3y + 4 = 0 và 2x + 3y - 1 = 0
Giải hệ được x = -1 với y = 1 ⇒ A(-1;1)
- Khoảng cách từ điểm A(-1;1) cho đường trực tiếp ∆: 3x + y + 16 = 0 là:
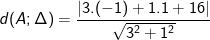
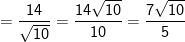
* lấy ví dụ 7: Trong mặt phẳng hệ tọa độ Oxy, đến tam giác ABC tất cả A(1;1); B(0;3) cùng C(4;0).
a) Tính chiều dài con đường cao AH (H thuộc BC).
b) Tính diện tích tam giác ABC
* Lời giải:
a) Tính chiều nhiều năm con đường cao AH
- Chiều lâu năm mặt đường cao AH chính là khoảng cách trường đoản cú A tới đường trực tiếp BC. Vì vậy ta đề nghị viết phương thơm trình nhường nhịn thẳng BC tự đó tính khoảng cách tự A tới BC.
- PT con đường trực tiếp BC: Đi qua B(0;3) với gồm CTCP BC(xC - xB; yC - yB) = (4;-3) đề xuất VTPT là n(3;4).
⇒ PTĐT (BC) là: 3(x - 0) + 4( y - 3) = 0 ⇔ 3x + 4y - 12 = 0
⇒ chiều cao của tam giác kẻ tự đỉnh A chính là khoảng cách từ điểm A cho đường trực tiếp BC:
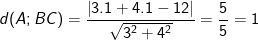
b) Tính diện tích S tam giác ABC.
- Ta có: SΔABC = (1/2).AH.BC
- Có độ lâu năm BC là:
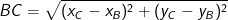
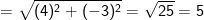
- Mà AH = d(A;BC) = 1 (theo câu a)
⇒ SΔABC = (1/2).AH.BC = (1/2).1.5 = 5/2 =2,5.
bởi thế, bài toán tính khoảng cách từ bỏ điểm M cho tới đường thẳng Δ đó là đồng nghĩa tương quan với câu hỏi tính độ nhiều năm của đoạn trực tiếp MH (H là hình chiếu của M lên Δ, tức MH ⊥ Δ).
Xem thêm: Cách Chỉnh Màu Trên Điện Thoại Samsung, Sử Dụng Chế Độ Màu Tối Trên Điện Thoại Android
Hy vọng cùng với nội dung bài viết tính khoảng cách giữa 2 điểm và từ là một điểm cho tới mặt đường thẳng nghỉ ngơi bên trên, các em sẽ hiểu rõ cùng áp dụng giải được những bài bác tập dạng này. Qua đó giúp những em chuẩn bị xuất sắc kỹ năng và kiến thức cho bài bác tính khoảng cách giữa 2 phương diện phẳng, 2 mặt đường trực tiếp tốt từ 1 điểm cho tới khía cạnh phẳng.