Các Cách Chứng Minh Hình Bình Hành

Trong bài viết này, các em sẽ tiến hành cung cấp hai phần hiếm hoi là lý thuyết cùng bài tập. Lý tmáu là những định nghĩa cùng đặc điểm về hình bình hành cũng như những dấu hiệu để nhận thấy hình bình hành nhưng các em đã được học tập bên trên lớp, bổ sung cập nhật thêm một vài kiến thức nâng cao nhằm củng nắm. Phần bài tập là các bài tập sách giáo khoa kèm theo phía dẫn giải chi tiết góp những em ôn luyện lại.

Bạn đang xem: Các cách chứng minh hình bình hành

LÝ THUYẾT VÀ BÀI TẬPhường HÌNH BÌNH HÀNH

A. Lý thuyết

1. Định nghĩa

Hình bình hành là tứ giác gồm các cạnh đối tuy vậy song.

ABCD là hình bình hành ⇔">⇔ AB // CD và AD // BC.

vì vậy, hình bình hành là hình thang tất cả nhị lân cận tuy nhiên tuy nhiên.

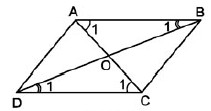
2. Tính chất

Định lí: 

Trong hình bình hành thì:

a) Các cạnh đối đều nhau.

b) Các góc đối bằng nhau.

c) Hai đường chéo giảm nhau trên trung điểm của mỗi con đường.

3. Dấu hiệu dấn biết

B. BÀI TẬP

Bài 1. Các tứ đọng giác ABCD, EFGH, MNPQ trên giấy kẻ ô vuông sinh sống hình 71 có là hình bình hành xuất xắc không?

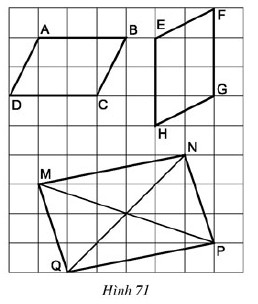
Lời giải:

Cả cha tđọng giác là hình bình hành

- Tđọng giác ABCD là hình bình hành vày gồm AB // CD với AB = CD = 3 (dấu hiệu nhận thấy 3)

- Tứ giác EFGH là hình bình hành vì tất cả EH // FG với EH = FH = 3 (dấu hiệu phân biệt 3)

- Tứ đọng giác MNPQ là hình bình hành vị có MN = PQ cùng MQ = NPhường (dấu hiệu phân biệt 2)

(Chú ý:

- Với những tđọng giác ABCD, EFGH còn có thể nhận biết là hình bình hành bởi dấu hiệu nhận ra 2.

- Với tđọng giác MNPQ còn hoàn toàn có thể nhận thấy là hình bình hành bằng tín hiệu nhận biết 5.)

Bài 2: Cho hình bình hành ABCD. Điện thoại tư vấn E là trung điểm của AD, F là trung điểm của BC. Chứng minc rằng BE = DF

Lời giải:

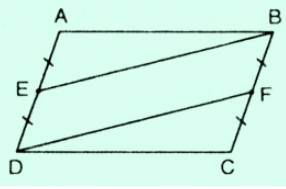
Ta có:

DE = 1/2.AD; BF = một nửa.BC

Mà AD = BF (ABCD là hình bình hành)

=> DE = BF

Tứ giác BEDF có:

DE // BF (do AD // BC)

DE = BF

Nên BEDF là hình bình hành suy ra BE = DF

Bài 3: Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ngơi nghỉ E, tia phân giác của góc B giảm CD làm việc F.

a) Chứng minc rằng DE // BF

b) Tứ đọng giác DEBF là hình gì? Vì sao?

Lời giải:

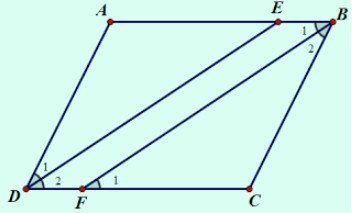
a) Ta gồm :

B^=D^">Bˆ=Dˆ (Vì ABCD">ABCDABCD là hình hành) (1)

B1^=B2^=B2^">B1ˆ=B2ˆ (vì BF">BFBF là tia phân giác góc B">BB) (2)

D1^=D2^=D^2">D1ˆ=D2ˆ (vì DE">DEDE là tia phân giác góc D">DD) (3)

Từ (1), (2), (3) ⇒D2^=B1^">⇒D2ˆ=B1ˆ, nhưng nhì góc này ở đoạn so le vào bởi vì đó: DE//BF">DE//BFDE//BF (*)

b) Tđọng giác DEBF có:

DE // BF (minh chứng sinh sống câu a)

BE // DF (vày AB // CD)

Nên theo quan niệm DEBF là hình bình hành.

Xem thêm: Hướng Dẫn Cách Đặt Tên Sản Phẩm Shopee Chuẩn Và Thu Hút Khách Hàng

Bài 4: Các câu sau đúng tốt sai?

a) Hình thang có nhị cạnh lòng đều nhau là hình bình hành

b) Hình thang bao gồm hai bên cạnh tuy nhiên song là hình bình hành

c) Tđọng giác gồm nhị cạnh đối đều nhau là hình bình hành

d) Hình thang bao gồm hai sát bên đều nhau là hình bình hành

Lời giải:

a) Đúng, vị hình thang có nhì đáy song tuy nhiên lại sở hữu thêm nhị cạnh lòng cân nhau phải là hình bình hành theo dấu hiệu phân biệt 5

b) Đúng, bởi lúc ấy ta được tđọng giác có các cạnh đối song tuy nhiên là hình bình hành (định nghĩa)

c) Sai, vì chưng hình thang cân có nhì cạnh đối (nhị cạnh bên) cân nhau tuy nhiên nó không phải là hình bình hành

d) Sai, bởi hình thang cân nặng gồm nhị kề bên cân nhau tuy vậy nó không hẳn là hình bình hành.

Bài 5: Cho hình 72. Trong đó ABCD là hình bình hành

a) Chứng minh rằng AHCK là hình bình hành

b) hotline O là trung điểm của HK. Chứng minch rằng cha điểm A, O, C thẳng hàng.

Lời giải:

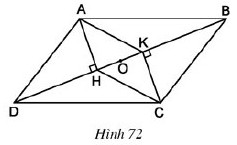
a) Hai tam giác vuông AHD với CKD có:

AD = CB (gt)

∠D1 = ∠B1 (so le trong)

Nên ∆AHD = ∆CKB (cạnh huyền, góc nhọn)

Suy ra AH = CK

Tđọng giác AHCK có AH // CK, AH = CK nên là hình bình hành,

b) Xét hìnhbìnhhành AHCK, trung điểm O của đường chéo của hìnhbìnhhành). Do đó cha điểm A, O, C trực tiếp sản phẩm.

Bài 6: Tứ giác ABCD tất cả E, F, G, H theo máy tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ đọng giác EFGH là hình gì? Vì sao?

Lời giải:

Tứ đọng giác EFGH là hình-bình -hành.

Cách 1: EB = EA, FB = FC (gt)

yêu cầu EF là mặt đường vừa đủ của ∆ABC.

Do đó EF // AC

Tương trường đoản cú HG là con đường trung bình của ∆ACD.

Do kia HG // AC

Suy ra EF // HG (1)

Tương từ bỏ EH // FG (2)

Từ (1) cùng (2) suy ra EFGH là hình -bình-hành (vệt hiêu nhận thấy 1).

Cách 2: EF là mặt đường mức độ vừa phải của ∆ABC đề nghị EF = một nửa AC.

HG là đường vừa đủ của ∆ACD buộc phải HG = 1/2 AC.

Suy ra EF = HG

Lại bao gồm EF // HG ( chứng minh trên)

Vậy EFGH là hình-bình-hành (dấu hiệu nhận ra 3).

Bài 7: Cho hình bình hành ABCD. Hotline I, K theo đồ vật trường đoản cú là trung điểm của CD, AB. Đường chéo cánh BD cắt AI, CK theo trang bị từ bỏ sinh hoạt M cùng N. Chứng minh rằng:

a) AI // CK

b) DM = MN = NB

Lời giải:

a) Tđọng giác ABCD tất cả AB = CD, AD = BC buộc phải là hình bình hành.

Tđọng giác AICK bao gồm AK // IC, AK = IC bắt buộc là hình bình hành.

Do đó AI // CK

b) ∆Dcông nhân gồm DI = IC, IM // công nhân.

Xem thêm: Cách Làm Gà Rán Sốt Chua Ngọt, 2 Cách Làm Gà Sốt Chua Ngọt Ngon Ai Ăn Cũng Thích

(vì chưng AI // CK) đề nghị suy ra DM = MN

Chứng minch tương tự so với ∆ABM ta gồm MN = NB.

Vậy DM = MN = NB

Tải về