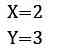Cách Giải Hệ Phương Trình Tuyến Tính
những phương trình con đường tính chúng là những phương thơm trình đa thức với một hoặc một vài ẩn số. Trong ngôi trường vừa lòng này, các ẩn số không được nâng lên thành các lũy quá, chúng cũng không được nhân cùng nhau (trong ngôi trường hòa hợp này bạn ta nói rằng pmùi hương trình là bậc 1 hoặc bậc 1).
Bạn đang xem: Cách giải hệ phương trình tuyến tính
Một phương thơm trình là 1 trong những đẳng thức toán học tập trong đó tất cả một hoặc những bộ phận chưa biết cơ mà họ vẫn gọi là ẩn số hoặc ẩn số vào trường đúng theo có khá nhiều hơn một. Để giải phương trình này, cần được tìm thấy quý hiếm của ẩn số.
Một phương trình tuyến tính tất cả cấu trúc sau:
một0· 1 + a1· X1+ một2· X2+... + an· Xn= b
Tại đâu0, một1, một2,..., mộtn là rất nhiều số thực mà lại họ biết giá trị của chúng cùng được Call là thông số, b cũng là một số trong những thực được nghe biết được Gọi là số hạng độc lập. Và ở đầu cuối họ là X1, X2,..., Xn kia là những gì được Điện thoại tư vấn là ẩn số. Đây là những vươn lên là có mức giá trị không xác định.
Một hệ pmùi hương trình tuyến tính là 1 trong những tập vừa lòng các phương trình con đường tính trong các số ấy cực hiếm của ẩn số là kiểu như nhau trong những phương thơm trình.
Về khía cạnh súc tích, giải pháp giải quyết và xử lý một hệ pmùi hương trình tuyến tính là gán cực hiếm mang đến ẩn số, nhằm hoàn toàn có thể xác minc đẳng thức. Điều đó Có nghĩa là, các ẩn số đề xuất được xem toán để tất cả các phương thơm trình của khối hệ thống được tiến hành đồng thời. Chúng tôi trình bày một hệ phương thơm trình con đường tính nhỏng sau
một0· 1 + a1· X1 + một2· X2 +... + an· Xn = an + 1
b0· 1 + b1· X1 + b2· X2 +... + bn· Xn = bn + 1
c0· 1 + c1· X1 + c2· X2 +... + cn· Xn = cn + 1
... .
d0· 1 + d1· X1 + d2· X2 +... + Dn· Xn = dn + 1
địa điểm một0, một1,..., mộtn,b0,b1,..., bn ,c0 ,c1,..., cn vv chúng tôi số thực và phần đa điều không biết nhằm giải quyết là X0,..., Xn ,Xn + 1.
Mỗi phương thơm trình tuyến tính thay mặt đại diện cho một cái và vì thế một hệ pmùi hương trình của N pmùi hương trình tuyến tính đại diện mang lại N trực tiếp được vẽ vào không gian.
Tùy nằm trong vào con số ẩn số mà lại mỗi phương trình đường tính bao gồm, con đường màn trình diễn pmùi hương trình vẫn nói sẽ được màn biểu diễn theo một chiều không giống nhau, nghĩa là một trong pmùi hương trình gồm hai ẩn số (ví dụ: 2 · X1 + X2 = 0) thể hiện một loại vào không gian hai chiều, một pmùi hương trình có tía ẩn số (ví dụ 2 · X1 + X2 - 5 · X3 = 10) sẽ tiến hành màn trình diễn trong không gian tía chiều, v.v..
khi giải hệ phương trình, những quý giá của X0,..., Xn ,Xn + 1 xảy ra là những điểm giảm thân các dòng.
Bằng biện pháp giải một hệ phương trình, bạn cũng có thể đi tới các Kết luận khác nhau. Tùy nằm trong vào một số loại hiệu quả nhưng mà Shop chúng tôi thu được, Cửa Hàng chúng tôi có thể phân biệt giữa 3 loại hệ pmùi hương trình tuyến tính:
1- Khả năng tương hợp ko xác định
Mặc mặc dù nghe dường như nlỗi một trò đùa, dẫu vậy rất có thể lúc nỗ lực giải hệ phương thơm trình, bọn họ đang đi mang đến một sự cụ thể về dạng hình 0 = 0.
Loại trường hợp này xẩy ra khi có các giải pháp vô hạn mang đến hệ phương trình, cùng vấn đề này xẩy ra Khi nó cho là trong hệ phương thơm trình của họ, các pmùi hương trình đại diện cho và một mẫu. Chúng ta hoàn toàn có thể thấy nó bằng đồ vật họa:
Là một hệ phương thơm trình, chúng tôi thực hiện:
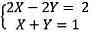
Bằng bí quyết có 2 phương thơm trình cùng với 2 ẩn số để giải, bạn có thể trình diễn các con đường thẳng vào phương diện phẳng hai chiều
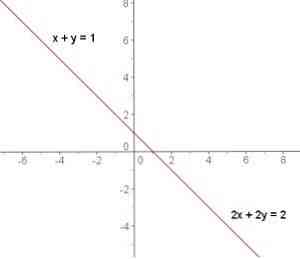
Nhỏng chúng ta cũng có thể thấy các mặt đường trực tiếp kiểu như nhau, vì vậy toàn bộ những điểm của pmùi hương trình thứ nhất trùng cùng với các phương trình đồ vật nhị, cho nên, nó có không ít điểm giảm nlỗi các điểm cơ mà con đường thẳng có, sẽ là những điểm vô hạn.
2- Không tương thích
Lúc hiểu thương hiệu bạn có thể tưởng tượng rằng hệ pmùi hương trình tiếp sau của chúng ta đang không tồn tại giải thuật.
Nếu họ nỗ lực giải, ví dụ, hệ phương thơm trình này
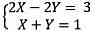
Về mặt bối cảnh, nó đã là:
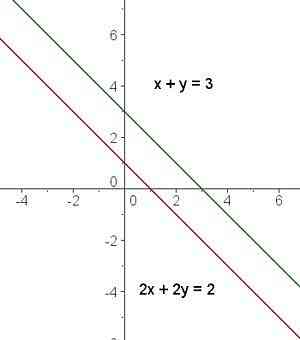
Nếu bọn họ nhân toàn bộ các số hạng của phương thơm trình lắp thêm hai, họ nhận được X + Y = 1 bằng 2 · X + 2 · Y = 2. Và trường hợp biểu thức ở đầu cuối này được trừ khỏi pmùi hương trình đầu tiên, họ thu được
2 · X-2 · X + 2 · Y -2 · Y = 3-2
Hoặc hồ hết gì tương tự nhau
0 = 1
khi bọn họ sinh hoạt trong trường hợp này, điều đó có nghĩa là những đường được biểu diễn vào hệ phương thơm trình là tuy vậy song, Có nghĩa là theo tư tưởng, bọn chúng ko lúc nào bị giảm cùng không tồn tại điểm giảm. khi một khối hệ thống được trình bày theo cách này, nó biết tới tự do ko đồng nhất.
3- Xác định hỗ trợ
Cuối thuộc bọn họ mang lại ngôi trường đúng theo hệ pmùi hương trình của bọn họ bao gồm một nghiệm độc nhất vô nhị, ngôi trường phù hợp họ gồm những đường giao nhau và tạo nên một nút giao nhau. Hãy xem một ví dụ:
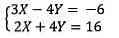
Để giải quyết chúng ta cũng có thể thêm hai pmùi hương trình để có được
(3 · X-4 · Y) + (2 · X + 4 · Y) = -6 + 16
Nếu bọn họ đơn giản và dễ dàng hóa, bọn họ đang rời đi
5 · X + 0 · Y = 5 · X = 10
Từ kia họ thuận tiện suy ra rằng X = 2 với thay thế hoặc X = 2 trong ngẫu nhiên phương trình lúc đầu nào bọn họ chiếm được Y = 3.
Xem thêm: Các Cách Trị Ợ Chua Tại Nhà, 10 Mẹo Chữa Ợ Hơi Hiệu Nghiệm Tức Thời
Trực quan liêu nó đã là:
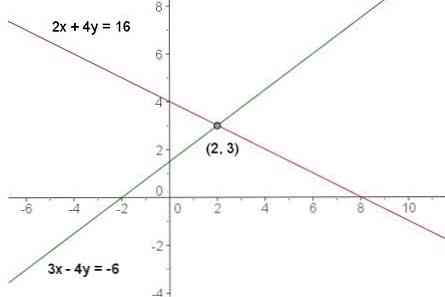
Phương phdẫn giải hệ phương trình con đường tính
Nhỏng chúng ta vẫn thấy trong phần trước, so với các hệ thống gồm 2 ẩn số cùng 2 pmùi hương trình, dựa trên các thao tác đơn giản nhỏng cộng, trừ, nhân, phân chia và sửa chữa thay thế, bạn cũng có thể xử lý chúng trong vài phút ít. Nhưng nếu như chúng ta cố gắng áp dụng phương pháp này cho các hệ thống có nhiều phương trình cùng nhiều ẩn số rộng, những phxay tính trnghỉ ngơi phải tẻ nhạt và chúng ta có thể thuận tiện mắc lỗi.
Để đơn giản và dễ dàng hóa các tính toán thù, có một trong những phương thức giải quyết, nhưng lại chắc chắn rằng các cách thức phổ biến nhất là Quy tắc của Cramer và Loại bỏ Gauss-Jordan..
Phương pháp nhồi nhét
Để phân tích và lý giải phương pháp vận dụng phương thức này, điều quan trọng là phải ghi nhận ma trận của chính nó là gì và biết phương pháp search định thức của nó, hãy tạo nên vệt ngoặc solo để xác định nhì khái niệm này.
Một ma trận nó không tồn tại gì không giống rộng là 1 trong tập đúng theo các số hoặc cam kết hiệu đại số được đặt trong số đường ngang với dọc cùng được sắp xếp theo phương thức hình chữ nhật. Đối với chủ đề của Shop chúng tôi, chúng tôi vẫn thực hiện ma trận nhỏng một giải pháp dễ dàng và đơn giản hơn để mô tả hệ phương trình của công ty chúng tôi.
Hãy coi một ví dụ:
Nó đã là hệ phương thơm trình đường tính
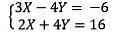
Hệ phương trình đơn giản và dễ dàng này chúng ta cũng có thể bắt tắt là hoạt động vui chơi của nhì ma trận 2 × 2 dẫn cho ma trận 2 × 1.
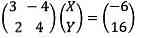
Ma trận thứ nhất tương ứng cùng với tất cả những thông số, ma trận máy nhị là ẩn số phải giải và ma trận nằm sau đẳng thức được xác định với những pháp luật tự do của phương thơm trình
các nguyên tố quyết định là một trong vận động được áp dụng cho một ma trận gồm công dụng là một trong những thực.
Trong ngôi trường phù hợp ma trận nhưng mà bọn họ sẽ kiếm tìm thấy trong ví dụ trước, nhân tố đưa ra quyết định của nó đang là:
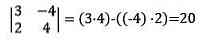
Khi các định nghĩa về ma trận với định thức đã có được xác minh, chúng ta có thể lý giải cách làm Cramer bao hàm mọi gì.
Bằng cách thức này, chúng ta có thể dễ ợt giải một hệ phương trình đường tính miễn là hệ ko thừa quá bố pmùi hương trình với ba ẩn số vì câu hỏi tính tân oán các định thức của ma trận hết sức khó khăn so với ma trận 4 × 4 hoặc cao hơn. Trong trường thích hợp bao gồm một khối hệ thống có nhiều hơn bố phương trình tuyến tính, phải thực hiện phương thức thải trừ Gauss-Jordan.
Tiếp tục cùng với ví dụ trước, bởi phương tiện đi lại của Cramer, họ chỉ topgamedanhbai.comệc tính hai yếu tố ra quyết định cùng với nó, họ vẫn kiếm tìm thấy quý hiếm của hai ẩn số của bọn họ.
Chúng tôi có hệ thống của chúng tôi:
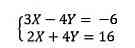
Và Shop chúng tôi tất cả một khối hệ thống được thay mặt đại diện bởi ma trận:
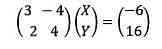
Giá trị của X được tra cứu thấy:
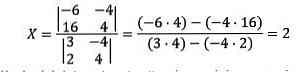
Đơn giản là vào tính toán thù của yếu tố đưa ra quyết định nằm trong chủng loại số của phnghiền chia, Shop chúng tôi sẽ thay thế làng đầu tiên cho ma trận những thuật ngữ hòa bình. Và vào mẫu số của phnghiền phân tách, họ bao gồm định thức của ma trận cội.
Thực hiện tại những phép tính tương tự nhằm kiếm tìm Y bọn họ thu được:
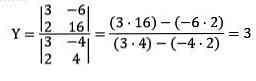
Loại vứt Gauss-Jordan
Chúng tôi khẳng định ma trận mở rộng mang đến ma trận công dụng xuất phát từ một hệ pmùi hương trình trong số ấy chúng ta thêm các thuật ngữ độc lập vào thời điểm cuối ma trận.
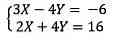
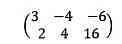
Phương pháp loại bỏ Gauss-Jordan bao gồm, bằng những cách thức chuyển động thân những hàng của ma trận, nhằm đổi khác ma trận không ngừng mở rộng của họ thành một ma trận dễ dàng và đơn giản hơn nhiều trong số ấy tôi bao gồm những số 0 trong toàn bộ những ngôi trường trừ vào con đường chéo, địa điểm tôi bắt buộc đem một vài. Nhỏng sau:

Trong số đó X với Y vẫn là những số thực khớp ứng với ẩn số của chúng ta.
Hãy giải quyết và xử lý khối hệ thống này bằng cách vứt bỏ Gauss-Jordan:
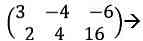
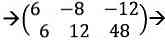
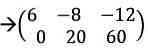
Chúng tôi sẽ làm chủ để sở hữu được số 0 tại vị trí bên dưới phía bên trái của ma trận, bước tiếp theo là lấy số 0 tại vị trí bên trên bên nên của chính nó.
Xem thêm: Top 5 Cách Làm Vòng Tay Bằng Chỉ Thêu Đơn Giản, Cách Làm Vòng Tay Handmade
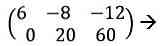
Chúng tôi đã đạt được 0 ở phía trên bên trái của ma trận, bây chừ chúng tôi chỉ phải biến đổi đường chéo thành mặt đường chéo cánh cùng công ty chúng tôi vẫn giải quyết và xử lý khối hệ thống của Shop chúng tôi bởi Gauss-Jordan.
Vì vậy, Shop chúng tôi đi mang đến kết luận rằng: