Home / Tin tức / cách giải phương trình lượng giác

Cách giải phương trình lượng giác

  admin  -     05/11/2021   190
Các dạng toán phương trình lượng giác, cách thức giải cùng bài xích tập tự cơ bản đến nâng cấp - toán lớp 11

Sau Khi làm cho quen cùng với những hàm lượng giác thì các dạng bài xích tập về phương thơm trình lượng giác chính là câu chữ tiếp sau nhưng mà những em sẽ học tập vào công tác tân oán lớp 11.

Bạn đang xem: Cách giải phương trình lượng giác


Vậy phương trình lượng giác gồm các dạng toán thù làm sao, phương pháp giải ra sao? bọn họ thuộc tìm hiểu qua bài viết này, mặt khác áp dụng các phương pháp giải này để triển khai các bài tập tự cơ bản đến nâng cao về phương thơm trình lượng giác.

I. Lý tngày tiết về Phương thơm trình lượng giác

1. Phương thơm trình sinx = a. (1)

° |a| > 1: Pmùi hương trình (1) vô nghiệm

° |a| ≤ 1: gọi α là một cung thỏa sinα = a, lúc đó phương trình (1) gồm các nghiệm là:

 x = α + k2π, ()

 cùng x = π - α + k2π, ()

- Nếu α vừa lòng điều kiện 

*
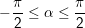
 cùng sinα = a thì ta viết α = arcsina. Khi đó các nghiệm của pmùi hương trình (1) là:

 x = arcsimãng cầu + k2π, ()

 cùng x = π - arcsina + k2π, ()

- Pmùi hương trình sinx = sinβ0 tất cả những nghiệm là:

 x = β0 + k3600, ()

 và x = 1800 - β0 + k3600, ()

2. Phương trình cosx = a. (2)

° |a| > 1: Phương thơm trình (2) vô nghiệm

° |a| ≤ 1: gọi α là 1 cung thỏa cosα = a, lúc đó phương trình (2) có các nghiệm là:

 x = ±α + k2π, ()

- Nếu α thỏa mãn ĐK 0 ≤ α ≤ π với cosα = a thì ta viết α = arccosa. Lúc đó những nghiệm của phương trình (2) là:

 x = ±arccosa + k2π, ()

- Phương thơm trình cosx = cosβ0 bao gồm các nghiệm là:

 x = ±β0 + k3600, ()

3. Phương trình tanx = a. (3)

- Tập xác minh, hay ĐK của phương trình (3) là: 

*

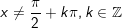
- Nếu α thỏa mãn nhu cầu điều kiện

*

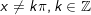
- Nếu α thỏa mãn nhu cầu ĐK

*

II. Các dạng toán về Phương trình lượng giác và cách thức giải

° Dạng 1: Giải phương trình lượng giác cơ bản

* Phương pháp

- Dùng những công thức nghiệm khớp ứng với mỗi phương trình.

* Ví dụ 1 (Bài 1 trang 28 SGK Đại số và Giải tích 11): Giải những pmùi hương trình sau:

a) b)

b)

d)

*

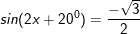
* Lời giải bài bác 1 trang 28 SGK Đại số và Giải tích 11:

a)  

*

 

*

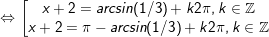
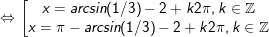
b) 

*

 

*

 

*

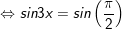
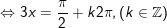
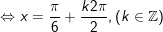
c) 

*

 

*

 

*

 

*

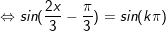
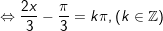
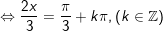
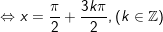
d)

*
 
*

 

*

*
*
 
*

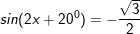
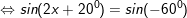
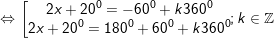
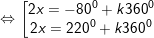
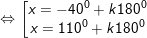
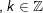
* ví dụ như 2: Giải những phương trình sau:

 a)

 b)

 c)

 d)

° Lời giải:

a) 

*

 

*
 
*
*

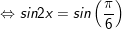
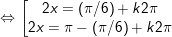
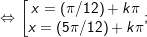
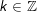
b) 

*

 

*
 
*
 
*

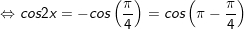
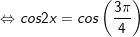
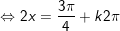
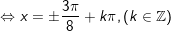
c) 

*

 

*
 
*

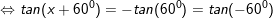
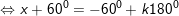
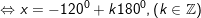
d) 

*

 

*
 
*

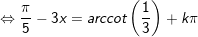
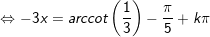
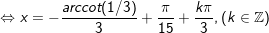
° Dạng 2: Giải một số phương trình lượng giác gửi được về dạng PT lượng giác cơ bản

* Phương thơm pháp

- Dùng những công thức biến đổi để đưa về phương thơm trình lượng giác vẫn mang lại về pmùi hương trình cơ bản nhỏng Dạng 1.

* lấy ví dụ 1: Giải các pmùi hương trình sau:

a) 

*

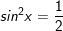
b) 

*

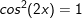
c) 

*

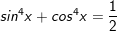
d) 

*

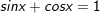
° Lời giải:

a)

*
 
*

 

*
*
 
*

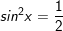
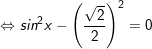
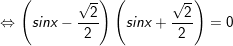
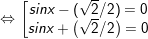
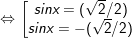
+ Với 

*
 
*
 hoặc 
*

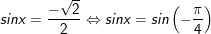
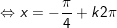
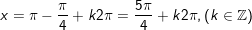
+ Với

*
 
*
 hoặc 
*

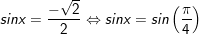
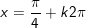
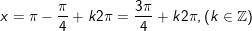
b) 

*
 
*

 

*
 
*

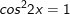
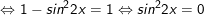
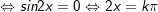
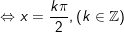
c)

*
 
*

 

*
 

 

*

 

*

 

*

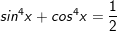
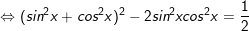
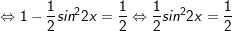
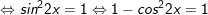
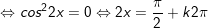
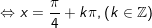
d)

*
*

 

*
 
*

 

*
 hoặc 
*

 

*

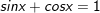
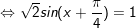
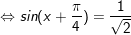
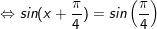
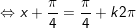
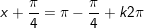
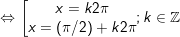
* Lưu ý: Bài toán thù bên trên áp dụng công thức:

 

*
*

 

*
*

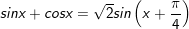
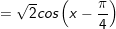
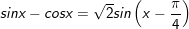
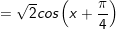
* ví dụ như 2: Giải các phương trình sau:

a) 

b)

° Lời giải:

a) 

 

*
*

 

*
 
*

 

*
 hoặc 
*
 với 
*

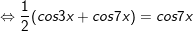
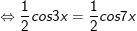
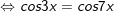
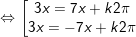
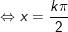
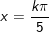
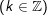
b)

 

*
 
*

 

*
 
*

 

*

 

*
 hoặc 
*
 với 
*

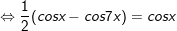
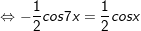
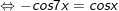
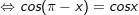
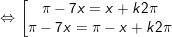
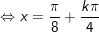
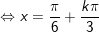
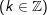
* Lưu ý: Bài tân oán áp dụng bí quyết chuyển đổi tích thành tổng:

 

*

 

*

 

*

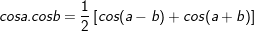
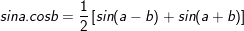
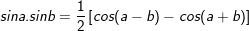
* ví dụ như 3: Giải các phương trình sau:

a)1 + 2cosx + cos2x = 0

b)cosx + cos2x + cos3x = 0

c)sinx + sin2x + sin3x + sin4x = 0

d)sin2x + sin22x = sin23x

° Lời giải:

a)

*

 

*
 
*

 

*
 
*

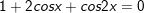
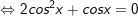
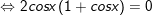
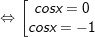
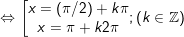
b)

*

 

*
 
*

 

*
*
 
*

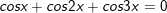
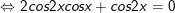
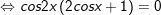
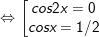
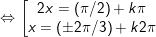
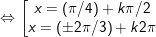
c)

*

 

*

 

*

 

*

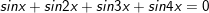
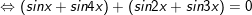
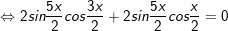
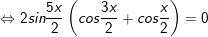
  hoặc 

*

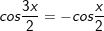
  hoặc 

*

 

*
 hoặc 
*
 hoặc 
*

 

*
 hoặc 
*
 hoặc 
*
 với 
*

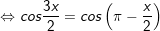
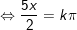
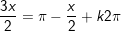
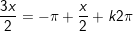
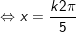
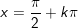
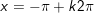
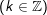
d)

*

 

*

 

*

 

*

 

*

 

*

 

*

 

*
 
*

 

*
 hoặc 
*
 hoặc 
*

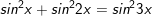
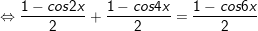
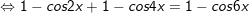
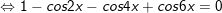
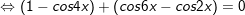
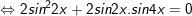
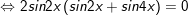
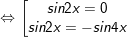
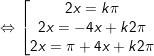
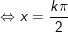
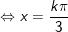
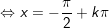
* Lưu ý: Bài tân oán trên có vận dụng phương pháp đổi khác tổng các kết quả và cách làm nhân đôi:

 

*

 

*

 

*

 

*

 

*

 

*
 
*

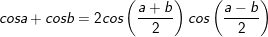
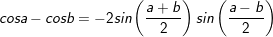
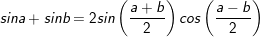
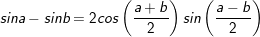
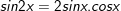
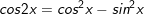
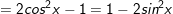
° Dạng 3: Phương trình hàng đầu gồm một hàm số lượng giác

* Phương pháp

- Đưa về dạng phương trình cơ bạn dạng, ví dụ: 

* lấy ví dụ như 1: Giải những phương thơm trình sau:

a) 

b) 

° Lời giải:

a)  

 

*
 
*

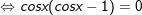
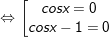
+ Với 

*

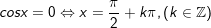
+ Với 

*

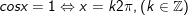
b)

 

*

 

*

 

*

 

*
 hoặc 
*

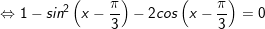
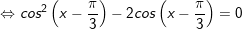
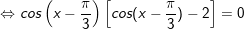
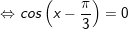
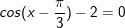
+ Với 

*
 
*
*

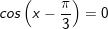
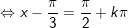
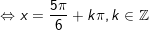
+ Với 

*
: vô nghiệm.

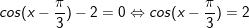
° Dạng 4: Pmùi hương trình bậc hai bao gồm một hàm con số giác

* Phương thơm pháp

♦ Đặt ẩn prúc t, rồi giải phương trình bậc hai đối với t, ví dụ:

 + Giải phương trình: asin2x + bsinx + c = 0;

 + Đặt t=sinx (-1≤t≤1), ta gồm phương trình at2 + bt + c = 0.

* Lưu ý: Lúc đặt t=sinx (hoặc t=cosx) thì phải tất cả điều kiện: -1≤t≤1

* lấy ví dụ 1: Giải các phương trình sau

a) 

b) 

° Lời giải:

a) 

- Đặt 

*
 ta có: 2t2 - 3t + 1 = 0

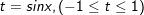
 ⇔ t = 1 hoặc t = 50%.

+ Với t = 1: sinx = 1 

*

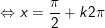
+ Với t=1/2: 

*
 

 

*
 hoặc 
*

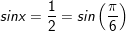
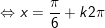
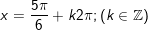
b) 

 

*

*

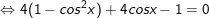
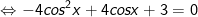
+ Đặt 

*
 ta có: -4t2 + 4t + 3 = 0

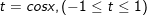
 ⇔ t = 3/2 hoặc t = -một nửa.

Xem thêm: Hướng Dẫn Cách Ứng Tiền Viettel Khi Còn Nợ, Cách Ứng Tiền Của Sim Viettel Khi Còn Nợ

+ t = 3/2 >1 đề xuất loại

+ 

*
*
 
*

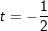
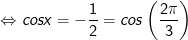
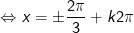
* Chụ ý: Đối với pmùi hương trình dạng: asin2x + bsinx.cosx + c.cos2x = 0, (a,b,c≠0). Pmùi hương pháp giải nlỗi sau:

 - Ta có: cosx = 0 không hẳn là nghiệm của phương trình vày a≠0,

 Chia 2 vế mang đến cos2x, ta có:atan2x + btanx + c = 0 (được PT bậc 2 cùng với tanx)

 - Nếu phương trình dạng: asin2x + bsinx.cosx + c.cos2x = d thì ta thay d = d.sin2x + d.cos2x, với rút ít gọn gàng đưa về dạng bên trên.

° Dạng 5: Phương thơm trình dạng: asinx + bcosx = c (a,b≠0).

* Phương pháp

◊ Cách 1: Chia nhị vế phương trình cho , ta được:

 

 - Nếu  thì pmùi hương trình vô nghiệm

 - Nếu  thì đặt 

 (hoặc )

- Đưa PT về dạng:  (hoặc ).

 ◊ Cách 2: Sử dụng phương pháp sinx cùng cosx theo ;

 

 - Đưa PT về dạng pmùi hương trình bậc 2 đối với t.

* Lưu ý: PT: asinx + bcosx = c, (a≠0,b≠0) gồm nghiệm lúc c2 ≤ a2 + b2

• Dạng tổng quát của PT là:asin + bcos = c, (a≠0,b≠0).

* Ví dụ: Giải những pmùi hương trình sau:

a) 

b)

° Lời giải:

a) 

+ Ta có: 

*
 lúc đó:

  

*

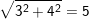
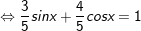
+ Đặt 

*
 ta có: cosφ.sinx + sinφ.cosx = 1.

 

*
 
*
 
*

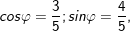
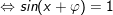
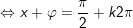
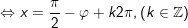
b) 

 

*
 
*

 

*

 

*
 hoặc 
*

 

*
 hoặc 
*

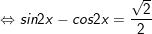
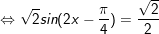
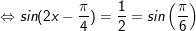
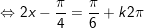
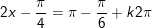
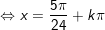
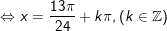
* Lưu ý: Bài toán thù áp dụng công thức:

 

*
 

 

*

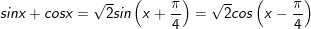
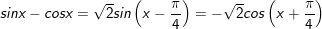
° Dạng 6: Phương thơm trình đối xứng với sinx với cosx

 a(sinx + cosx) + bsinx.cosx + c = 0 (a,b≠0).

Xem thêm: Cách Xử Lý Nước Hồ Cá Bị Đục, {Bật Mí} Cách Làm Nước Trong Hồ Cá Không Bị Đục

* Phương pháp

- Đặt t = sinx + cosx, Lúc đó:  cố gắng vào phương trình ta được:

 bt2 + 2at + 2c - b = 0 (*)

- Lưu ý: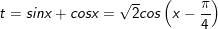 

*
 buộc phải ĐK của t là: 

- Do đó sau thời điểm tìm được nghiệm của PT (*) buộc phải chất vấn (đối chiếu) lại ĐK của t.

- Phương trình dạng: a(sinx - cosx) + bsinx.cosx + c = 0 không phải là PT dạng đối xứng cơ mà cũng rất có thể giải bằng phương pháp tương tự:

 Đặt t = sinx - cosx;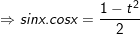  

*

* Ví dụ: Giải các phương thơm trình sau:

a) 2(sinx + cosx) - 4sinx.cosx - 1 = 0

b) sin2x - 12(sinx + cosx) + 12 = 0

° Lời giải:

a) 2(sinx + cosx) - 4sinx.cosx - 1 = 0

+ Đặt t = sinx + cosx, , lúc đó:   gắng vào phương thơm trình ta được:

 

*
 ⇔ 2t2 - 2t - 1 = 0

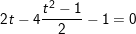
  hoặc 

+ Với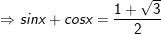  

*

 

*
 
*

 

*

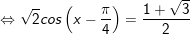
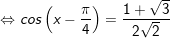
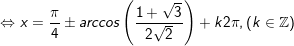
+ Tương từ bỏ, với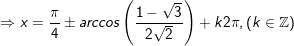 

*

 b) sin2x - 12(sinx + cosx) + 12 = 0

 

*

 

*

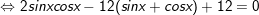
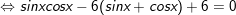
- Đặt t = sinx + cosx, , khi đó:   vắt vào phương thơm trình ta được:

 

*
 
*
 
*

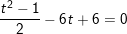
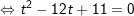
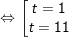
+ Với t=1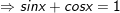 

*

 

*
*

 

*
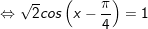
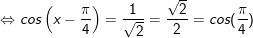
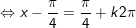
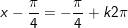
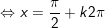
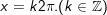
 hoặc 
*

*
 hoặc 
*

+ Với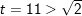 

*
: loại

III. các bài tập luyện về những dạng toán thù Pmùi hương trình lượng giác

* Bài 2 (trang 28 SGK Đại số với Giải tích 11): Với đông đảo quý hiếm như thế nào của x thì giá trị của những hàm số y = sin 3x cùng y = sin x bởi nhau?

° Lời giải bài xích 2 trang 28 SGK Đại số với Giải tích 11:

- Ta có: 

*

 

*
 
*

 

*

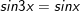
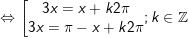
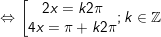
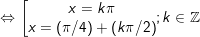
- Vậy với 

*
thì 
*

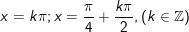
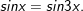
* Bài 3 (trang 28 SGK Đại số 11): Giải những phương thơm trình sau:

 a) 

 b) 

*

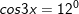
 c) 

 d) 

° Lời giải bài 3 trang 28 SGK Đại số với Giải tích 11:

a) 

 

*
 
*

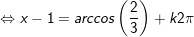
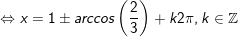
- Kết luận: PT có nghiệm

*

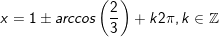
b) cos3x = cos12º

⇔ 3x = ±12º + k.360º , k ∈ Z

⇔ x = ±4º + k.120º , k ∈ Z

- Kết luận: PT bao gồm nghiệm x = ±4º + k.120º , k ∈ Z

c) 

 

*
 

 

*
 hoặc 
*

 

*
 hoặc 
*

 

*
 hoặc 
*

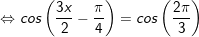
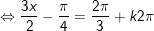
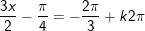
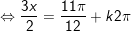
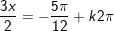
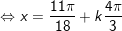
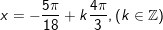
d) 

 

*
 hoặc 
*

 

*
 hoặc 
*

 

*
 hoặc 
*

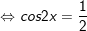
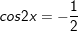
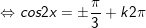
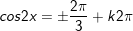
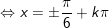
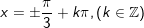
* Bài 4 (trang 29 SGK Đại số cùng Giải tích 11): Giải phương trình 

° Lời giải bài 3 trang 28 SGK Đại số với Giải tích 11:

- Điều kiện: sin2x≠1

- Ta có:  

*

 

*
 
*

 

*

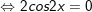
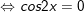
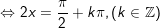
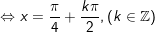
+ Đến đây ta cần so sánh với điều kiện:

- Xét k lẻ tức là: k = 2n + 1

 

*

*
(thỏa điều kiện)

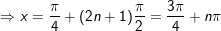
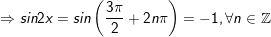
- Xét k chẵn tức là: k = 2n

*

*
 (không thỏa ĐK)

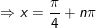
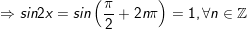
- Kết luận: Vậy PT bao gồm họ nghiệm là 

*

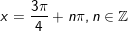
* Bài 1 (trang 36 SGK Đại số với Giải tích 11): Giải phương thơm trình: sin2x – sinx = 0 

° Lời giải bài 1 trang 36 SGK Đại số cùng Giải tích 11:

- Ta có: sin2x – sinx = 0

 

*

 

*
 
*

 

*
 hoặc 
*

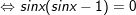
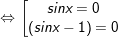
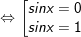
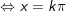
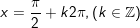
- Kết luận: PT gồm tập nghiệm 

*

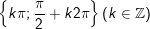
* Bài 2 (trang 36 SGK Đại số cùng Giải tích 11): Giải những phương trình sau:

a) 2cos2x – 3cosx + 1 = 0

b) 2sin2x +

*
.sin4x = 0

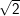
° Lời giải bài 2 trang 36 SGK Đại số và Giải tích 11:

a) 2cos2x – 3cosx + 1 = 0 (1)

- Đặt t = cosx, điều kiện: –1 ≤ t ≤ 1, lúc đó PT (1) trsống thành: 2t2 – 3t + 1 = 0

Copyright © 2021 topgamedanhbai.com