CÁCH TÍNH ĐỊNH THỨC CẤP 3
1. Phần bù đại số
Cho ma trận $A=(a_ij)_n imes n$ khi đó $A_ij=(-1)^i+jM_ij,$ với $M_ij$ là định thức nhận thấy từ định thức của ma trận $A$ bằng cách vứt đi cái $i$ với cột $j$ được Điện thoại tư vấn là phần bù đại số của bộ phận $a_ij.$
ví dụ như 1:Cho ma trận $A = left( eginarray*20c 1&2& - 1&m\ 3&1&4&2\ - 3&4&2&1\ - 1&2&1&3 endarray ight).$
Tính các phần bù đại số $A_11,A_12,A_13,A_14.$
Giải.
Bạn đang xem: Cách tính định thức cấp 3
Ta có:
$eginarrayl A_11 = ( - 1)^1 + 1left| eginarray*20c 1&4&2\ 4&2&1\ 2&1&3 endarray ight| = - 35;A_12 = ( - 1)^1 + 2left| eginarray*20c 3&4&2\ - 3&2&1\ - 1&1&3 endarray ight| = - 45;\ A_13 = ( - 1)^1 + 3left| eginarray*20c 3&1&2\ - 3&4&1\ - 1&2&3 endarray ight| = 34;A_14 = ( - 1)^1 + 4left| eginarray*20c 3&1&4\ - 3&4&2\ - 1&2&1 endarray ight| = 7. endarray$
Công thức khai triển Laplace
Cho ma trận $A=(a_ij)_n imes n$ lúc đó
$det (A)=a_i1A_i1+a_i2A_i2+...+a_inA_in ext (i=1,2,...,n)$
đấy là cách làm khai triển định thức ma trận $A$ theo cái lắp thêm $i.$
$det (A)=a_1jA_1j+a_2jA_2j+...+a_njA_nj ext (j=1,2,...,n)$
đó là phương pháp knhì triển định thức ma trận $A$ theo cộng trang bị $j.$
lấy ví dụ như 1: Tính định thức của ma trận $A = left( eginarray*20c 1&2& - 1&m\ 3&1&4&2\ - 3&4&2&1\ - 1&2&1&3 endarray ight)$ theo cách làm khai triển chiếc 1.
Giải. Có$det (A)=1.A_11+2.A_12-1.A_13+m.A_14,$ trong các số đó
$eginarrayl A_11 = ( - 1)^1 + 1left| eginarray*20c 1&4&2\ 4&2&1\ 2&1&3 endarray ight| = - 35;A_12 = ( - 1)^1 + 2left| eginarray*20c 3&4&2\ - 3&2&1\ - 1&1&3 endarray ight| = - 45;\ A_13 = ( - 1)^1 + 3left| eginarray*20c 3&1&2\ - 3&4&1\ - 1&2&3 endarray ight| = 34;A_14 = ( - 1)^1 + 4left| eginarray*20c 3&1&4\ - 3&4&2\ - 1&2&1 endarray ight| = 7. endarray$
Vậy $det (A)=-35+2.(-45)-34+7m=7m-159.$
ví dụ như 2: Tính định thức $left| eginarray*20c 1&1&2&2\ - 3&1&5&1\ - 2&5&0&0\ 2& - 1&3& - 1 endarray ight|.$
Giải. Để ý chiếc 3 của định thức tất cả 2 thành phần bởi 0 nên khai triển theo dòng này đang chỉ bao gồm nhị số hạng
Có
ví dụ như 3: Tính định thức $left| eginarray*20c 0&1&2& - m\ - 2& - 1&2&1\ 0& - 3&4&2\ 0& - 5&1&1 endarray ight|.$
Giải. Để ý cột 1 có 3 bộ phận bằng 0 buộc phải khai triển theo cột 1 ta có
lấy ví dụ 4: Tính định thức
Giải. Để ý cột 3 gồm phần tử đầu tiên là 1, vậy ta đã biến hóa sơ cấp cho cho định thức theo cột 3
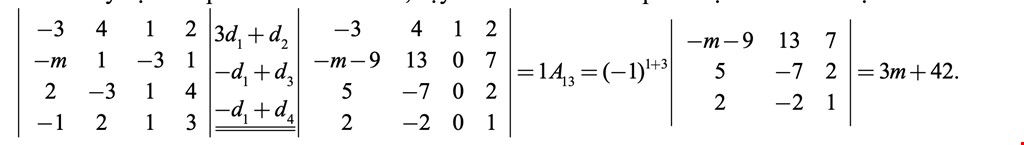
lấy một ví dụ 5: Tính định thức $left| eginarray*20c 1&2& - 3&4\ - 1&3&1& - m\ 2& - 4&3&1\ - 3&2&1&2 endarray ight|.$
Giải. Có
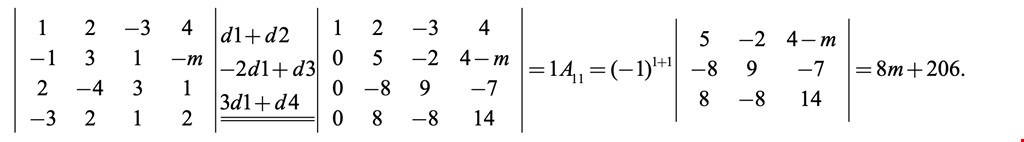
lấy ví dụ như 6: Cho ma trận $A = left( eginarray*20c 1&2& - 3&4\ - 1&3&1& - m\ - 2& - 2& - 2& - 2\ - 3&2&1&2 endarray ight).$ Tính tổng những phần bù đại số của những thành phần thuộc loại 4 của ma trận $A.$
Giải. Ttuyệt những bộ phận ở dòng 4 của ma trận A vày $-2,$ ta được ma trận $B = left( eginarray*20c 1&2& - 3&4\ - 1&3&1& - m\ - 2& - 2& - 2& - 2\ - 2& - 2& - 2& - 2 endarray ight)$ tất cả định thức bởi 0 vì chưng bao gồm hai loại giống nhau với nhị ma trận $A,B$ gồm các phần bù đại số của các thành phần mẫu 4 như là nhau.
Vậy $det (B)=-2A_41-2A_42-2A_43-2A_44=0Leftrightarrow A_41+A_42+A_43+A_44=0.$
lấy một ví dụ 7: Cho ma trận $A = left( eginarray*20c 1&2&3&4\ - 2& - 1&4&1\ 3& - 4& - 5&6\ - 4&5& - 6&7 endarray ight).$ Tính $A_41+2A_42+3A_43+4A_44.$
Giải. Tgiỏi những bộ phận làm việc mẫu 4 của ma trận A theo thứ tự vì $1,2,3,4$ ta được ma trận $B = left( eginarray*20c 1&2&3&4\ - 2& - 1&4&1\ 3& - 4& - 5&6\ 1&2&3&4 endarray ight)$ tất cả định thức bằng 0 bởi vì gồm nhì mẫu như thể nhau và nhì ma trận $A,B$ có các phần bù đại số của các thành phần chiếc 4 giống như nhau
Vậy $det (B)=1A_41+2A_42+3A_43+4A_44=0Leftrightarrow A_41+2A_42+3A_43+4A_44=0.$
lấy ví dụ 8: Cho D là 1 trong định thức cấp n tất cả tất cả những bộ phận của một dòng lắp thêm i bởi 1. Chứng minch rằng:
Tổng các phần bù đại số của những bộ phận thuộc từng cái không giống loại máy i phần lớn bằng 0.Định thức D bằng tổng phần bù đại số của tất cả những phần tử của nó.Xem thêm: Cách Làm Vòng Tay Bằng Dây Giày, Cách Làm Vòng Đeo Tay Bằng Dây Giày Đẹp Nhất
Ví dụ 9: Tính định thức $left| eginarray*20c - 2&5&0& - 1&3\ 1&0&3&7& - 2\ 3& - 1&0&5& - 5\ 2&6& - 4&1&2\ 0& - 3& - 1&2&3 endarray ight|.$
lấy ví dụ như 10: Tính định thức $left| eginarray*20c 1& - 2&3&2& - 5\ 2&1&2& - 1&3\ 1&4&2&0&1\ 3&5&2&3&3\ 1&4&3&0& - 3 endarray ight|.$
3. Định thức của ma trận tam giác
Định thức của ma trận tam giác bằng tích các thành phần nằm trên phố chéo chính
Thật vậy, so với ma trận tam giác trên knhì triển theo cột 1 có:
so với ma trận tam giác bên dưới knhị triển theo cái 1.
4. Tính định thức dựa trên những đặc thù định thức, công thức knhị triển Laplace và chuyển đổi về ma trận tam giác
Ví dụ 10: Tính định thức $left| eginarray*20c a&b&...&b\ b&a&...&b\ ...&...&...&...\ b&b&...&a endarray ight|.$
Giải. Ta có:
$eginarrayl left| eginarray*20c a&b&...&b\ b&a&...&b\ ...&...&...&...\ b&b&...&a endarray ight|underlineunderline c2 + c3 + ... + cn + c1 left| eginarray*20c a + (n - 1)b&b&...&b\ a + (n - 1)b&a&...&b\ ...&...&...&...\ a + (n - 1)b&b&...&a endarray ight|\ = left( a + (n - 1)b ight)left| eginarray*20c 1&b&...&b\ 1&a&...&b\ ...&...&...&...\ 1&b&...&a endarray ight|\ underlineunderline - d_1 + d_i left( a + (n - 1)b ight)left| eginarray*20c 1&b&...&b\ 0&a - b&...&b\ ...&...&...&...\ 0&0&...&a - b endarray ight| = left( a + (n - 1)b ight)(b - b)^n - 1. endarray$
Lúc Này topgamedanhbai.com kiến thiết 2 khoá học Tân oán cao cấp 1 cùng Toán thời thượng 2 dành cho sinh viên năm nhất hệ Cao đẳng, ĐH kăn năn ngành Kinch tế của tất cả những trường:
Khoá học hỗ trợ vừa đủ kỹ năng và phương pháp giải bài bác tập các dạng toán kèm theo từng bài học. Hệ thống bài bác tập rèn luyện dạng Tự luận bao gồm lời giải chi tiết tại website để giúp đỡ học tập viên học nhanh khô và vận dụng chắc chắn kiến thức. Mục tiêu của khoá học tập giúp học tập viên đạt điểm A thi cuối kì các học phần Tân oán cao cấp 1 và Tân oán thời thượng 2 trong các trường tài chính.
Xem thêm: Cách Chơi Bài Tấn Durak Dễ Hiểu Nhất, Bài Tấn Là Gì
Sinch viên những ngôi trường ĐH sau đây hoàn toàn có thể học tập được full bộ này:
- ĐH Kinh Tế Quốc Dân
- ĐH Ngoại Thương
- ĐH Tmùi hương Mại
- Học viện Tài Chính
- Học viện ngân hàng
- ĐH Kinch tế ĐH Quốc Gia Hà Nội
và những ngôi trường ĐH, ngành kinh tế của những trường ĐH không giống trên khắp toàn nước...