Cách Tính Khoảng Cách Từ 1 Điểm Đến 1 Đường Thẳng

Trong khía cạnh phẳng Oxy đến điểm $M(x_M;y_M)$ cùng con đường thẳng $Delta$ gồm phương thơm trình: $ax+by+c=0$. Khi kia khoảng cách từ bỏ điểm $M(x_M;y_M)$ mang đến con đường trực tiếp $Delta$ được xác minh bởi công thức:

$d(M,Delta)=dfracsqrta^2+b^2$

Khoảng giải pháp trường đoản cú điểm M mang lại mặt đường thẳng $Delta$ chính là đoạn MH với H là hình chiếu vuông góc của điểm M xuất xứ thẳng $Delta$.

Bạn đang xem: Cách tính khoảng cách từ 1 điểm đến 1 đường thẳng

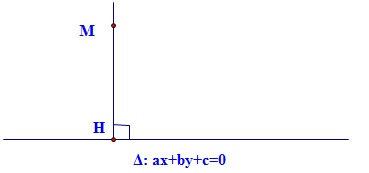
do vậy nhằm tính được khoảng cách tự điểm M đến con đường trực tiếp $Delta$ thì chúng ta rất cần phải khẳng định được 2 yếu hèn tố:

Bài thói quen khoảng cách từ 1 điểm đến lựa chọn một đường thẳng

Những bài tập 1: Trong khía cạnh phẳng Oxy mang đến con đường trực tiếp $Delta$ và đường trực tiếp a theo lần lượt gồm phương thơm trình là: $2x+3y-1=0$ cùng $4x+3y-5=0$

a. Tính khoảng cách tự điểm $M(2;1)$ cho đường thẳng $Delta$

b. Tính khoảng cách trường đoản cú điểm $A(2;4)$ mang lại con đường thẳng $a$

Hướng dẫn:

a. Khoảng cách từ điểm $M(2;1)$ mang đến đường thẳng $Delta$ là:

$d(M,Delta)=dfracsqrt2^2+3^2$

=> $d(M,Delta)=dfrac6sqrt13$

=> $d(M,Delta)=dfrac6sqrt1313$

b. Khoảng phương pháp tự điểm $A(2;4)$ đến mặt đường thẳng $a$ là:

$d(M,a)=dfracsqrt4^2+3^2$

=> $d(M,a)=dfrac15sqrt4^2+3^2$

=> $d(M,a)=dfrac155=3$

những bài tập 2: Cho tam giác ABC biết $A(1;2)$; $B(2;3)$; $C(-1;2)$. Tính độ dài con đường cao bắt đầu từ đỉnh A xuống cạnh BC.

Xem thêm: Cách Nấu Khoai Mì Nước Cốt Dừa Ngon Bá Chấy, Cách Làm Khoai Mì Nước Cốt Dừa

Hướng dẫn:

Độ dài mặt đường cao bắt đầu từ đỉnh A mang lại cạnh BC chính là khoảng cách trường đoản cú điểm A đến đường thẳng BC. Do đó ta yêu cầu viết được phương trình của con đường thẳng BC.

Xem thêm: Trưa Nay Ăn Gì: Cách Làm Gà Tần Ngải Cứu Tốt Cho Mẹ Bầu, Làm Gà Hầm Ngải Cứu Siêu Ngon Cho Ngày Mưa

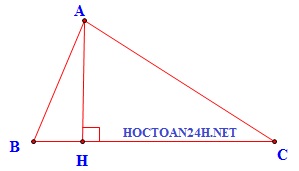
Ta có: $vecBC=(-3;-1)$

Vectơ pháp đường của con đường trực tiếp BC là: $vecn_BC=(1;-3)$

Đường thẳng BC đi qua điểm $B(2;3)$ có phương thơm trình là:

$1.(x-2)-3(y-3)=0$ $x-3y+7=0$

Khoảng phương pháp từ bỏ điểm $A(1;2)$ cho đường thẳng BC là:

$d(A,BC)=dfrac1-3.2+7sqrt1^2+(-3)^2$

=> $d(A,BC)=dfrac2sqrt10$

=> $d(A,BC)=dfracsqrt105$

Vậy độ nhiều năm mặt đường cao xuất phát điểm từ đỉnh A mang đến cạnh BC bằng: $dfracsqrt105$

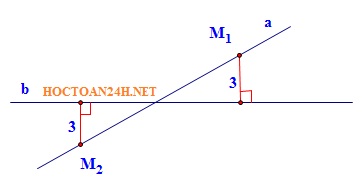
Bài tập 3: Tìm tất cả rất nhiều điểm nằm trên tuyến đường thẳng a gồm phương thơm trình: $x+y-3=0$ với bao gồm khoảng cách đến đường thẳng b có phương thơm trình $3x-4y+5=0$ bởi 3.

Hướng dẫn:

điện thoại tư vấn $M$ là vấn đề bất cứ thuộc đường thẳng a. khi đó ta bao gồm tọa độ của điểm $M$ là: $M(x_M;-x_M+3)$

Khoảng biện pháp tự điểm M cho con đường trực tiếp b là:

$d(M,b)=dfracsqrt3^2+(-4)^2$

=> $ d(M,b) = dfrac-x_M-75$

=> $ d(M,b) = dfracx_M+75$

Theo bài bác ra khoảng cách tự điểm M mang lại con đường trực tiếp b bởi 3 bắt buộc ta có:

$ dfracx_M+75=3$

$|x_M+7|=15$

$x_M+7=15$ hoặc $x_M+7=-15$

$x_M=8$ hoặc $x_M=-19$

Vậy tất cả nhì điểm M thuộc đường thẳng a và bao gồm khoảng cách đến con đường trực tiếp b bởi 3 là nhị điểm $M_1(8;-5)$ cùng $M_2(-22;-19)$

các bài luyện tập rèn luyện tính khoảng cách xuất phát điểm từ một điểm tới một mặt đường thẳng

những bài tập 1: trong phương diện phẳng Oxy đến con đường trực tiếp a cùng b theo lần lượt bao gồm phương trình là: $2x-3y+7=0$ với $4x+3y-11=0$.

a. Tính khoảng cách từ bỏ điểm $A(2;-3)$ cho tới con đường thẳng a

b. Tính khoảng cách trường đoản cú điểm $B(-4;3)$ cho tới mặt đường thẳng b

các bài luyện tập 2: Tính diện tích hình vuông gồm toạ độ một đỉnh là A(4;2) với phương thơm trình một mặt đường chéo cánh là $x+2y+2=0$

các bài luyện tập 3: Viết pmùi hương trình của đường thẳng a tuy vậy song với mặt đường thẳng b: 3x + 4y – 1 = 0 cùng cách đường thẳng b một đoạn bởi 2

Bài tập 4: Tìm bán kính của mặt đường tròn trung tâm I(2, –3) với tiếp xúc với mặt đường thẳng: 12x -5y +3 = 0